D10 Mechanical Counter

A Note to Readers:
Hi! Welcome to our second blog post! I promise they won't always only be about 3d printed things lol (but some certainly will). We do actually do other things too, but these were a couple of recent projects that were particularly fun to write about. Would love to hear what you think at the end if you'd like to drop us a comment.

As before (if you read the previous post) I'll be using hyperlinked footnotes to help keep the main post readable and organized. All of the links on this post simply jump to other places on this same page, and you can also find the footnotes section by scrolling to the bottom if you prefer.

D10 Mechanical Counter
byu/FuncFriv in3Dprinting

The video above demonstrates a thing I designed that I've been calling the "D10 Mechanical Counter". It is a mechanical counter that uses a ten-sided die (d10) as the means for displaying a value from 0-9. Basically it is a mechanism that holds a d10 and can manipulate it to present the numbered faces in sequential order. It can be used to track some incrementally changing value, especially in games (like D&D) that already make frequent use of these dice.

How Does It Work?

Being a mechanical counter, this device must be able to display the current value and increment by one when actuated. "Display" here means to orient the appropriate die face toward the user, so at this point I think its a good idea to briefly explore what a d10 is and how the numbers are arranged on the different faces. This will help to understand what actually needs to happen mechanically to get from one number to the next.

As mentioned above, a d10 is a ten-sided die, which is commonly used in D&D and other table-top games, as part of a larger set of "polyhedral" dice. It can naturally be thought of as being made up of two pyramid-ish halves, each with five kite-shaped faces. In the typical numbering layout, one of these halves contains all of the even numbers and the other contains the odds.

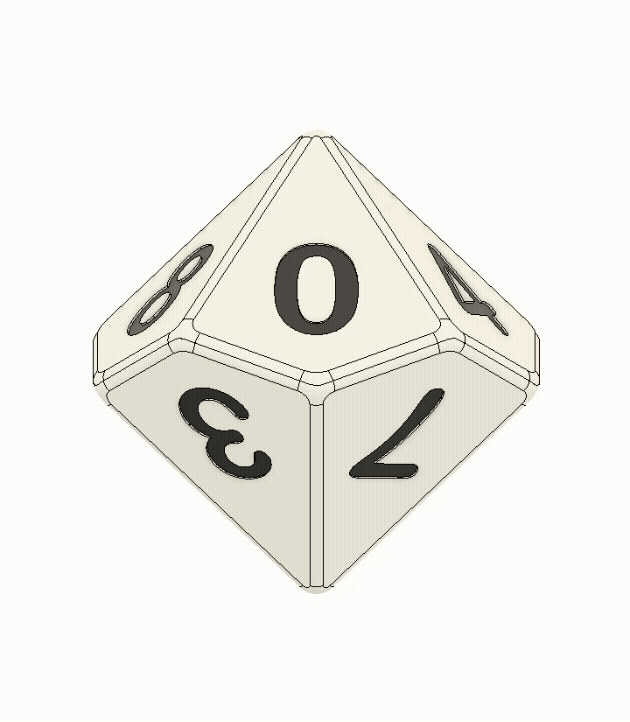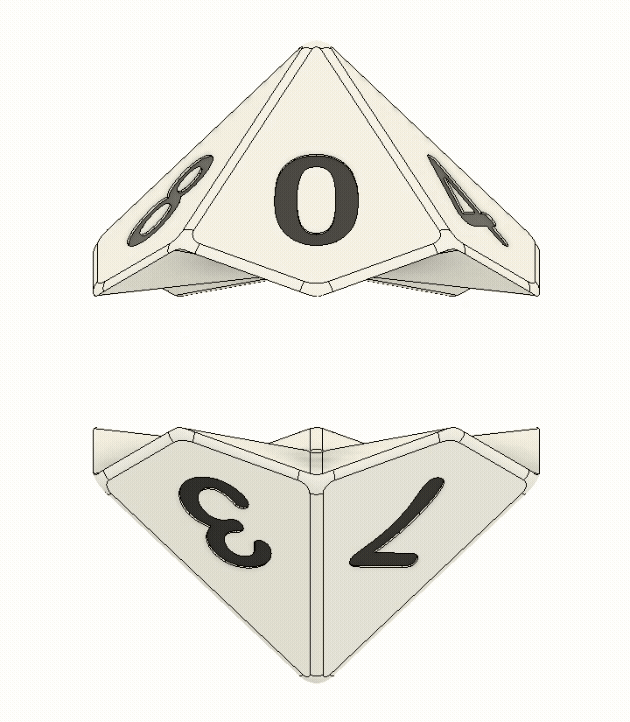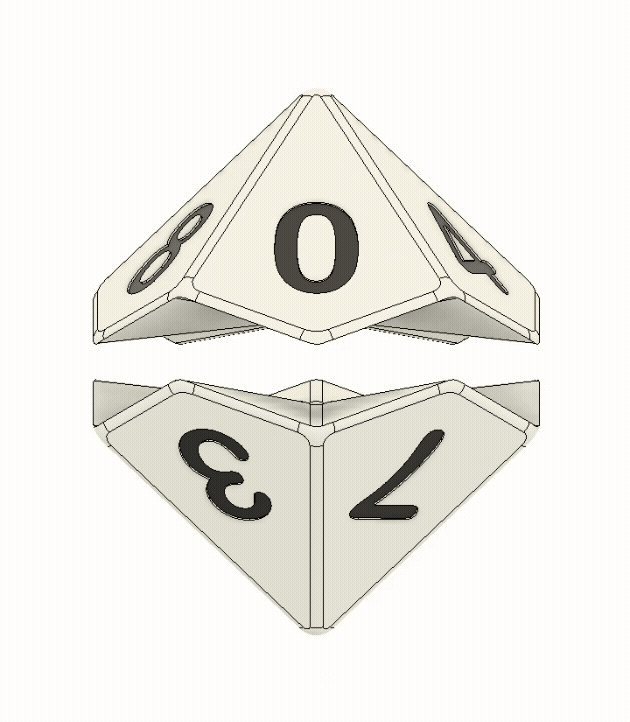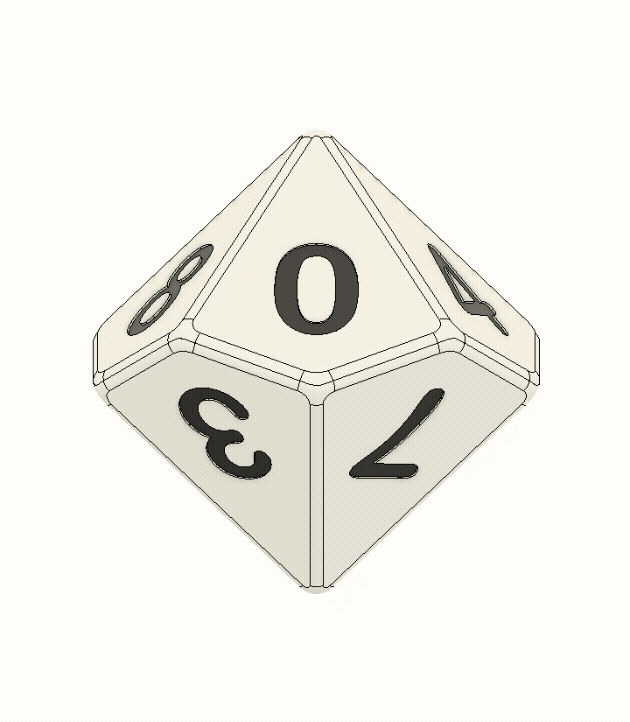
This already gives us our first critical requirement for the device: It needs to switch back and forth between the even half and the odd half as part of each increment. If you watch the device in operation, you can see that is exactly what it does. With each 180° rotation of the knob, the d10 gets flipped 180° counterclockwise.

But this alone is not enough. You might be thinking, "yeah obviously, if you keep flipping 180° you'll just alternate between the same two numbers". Well, its actually worse than that because the two halves of the die are offset by 36°, so you'd really just alternate between displaying one face and one edge. So, we need to be able to spin the die as well.

A quick bit of housekeeping to help us keep the terminology straight going forward: 
What I call "spin" here refers to rotation about the axis that passes through the points of the pyramids. What I'm calling "flip" is when the points themselves are rotated left/right.

Ok so we need to flip 180° every time and also spin some amount. Maybe we're lucky, and the numbers are arranged such that the amount of spin required is the same for each increment.... nope. Here's what we actually find when we look into how much spin it takes to get from each number to its successor:

That's three total spins that we need to account for: 108°, 180°, and 252°. Could be worse. And actually, these are just the values if we are restricted to spinning the die in only one direction. If we allow spin in either direction, we can think of the 252° rotation as equivalent to -108° (aka 360°-252°). If we take this perspective, we can say that we actually have two spin distances (180° and 108°) as well as two spin directions (+ and -). For reasons that will be discussed later, this is the approach that ended up being the most useful.

So, fundamentally what this device must do is rotate the d10 about two different axes (spin and flip). And while the flip is constant for every increment, the spin needs to be controlled specifically depending on which number is displayed.

Now we can get into how the device achieves these actions, and how each of the pieces are designed in order to facilitate that.

How to Flip

It should be obvious by now that the flip action is by far the simplest problem to solve, so we'll start here as we begin to explore the inner workings.

First of all, the die is held using two spool-shaped pieces with faceted cups that grip the d10 at its points. These spools are held by another component that constrains them in all degrees of freedom except for one direction of rotation, which will allow the die to spin. This component is the "Flip Carrier", as it carries the spools and die when it rotates to produce our flip action.

Since the input to this whole system is a rotating knob (we'll get into why later), what we need is to transform that vertical rotation into rotation on our horizontal flip axis. A natural solution here is a set of bevel gears, and that's exactly what we have. This is a pretty simple system, as expected, and there's honestly not much more to say about it.

How to Spin

This is what we've really been building toward... As before, we'll start at the die. Since we already have a die-holding system that allows spin, we just need to add some features to drive and control it. One of the spools gets a set of gear teeth for this purpose, and earns itself the name "Spinion" (as in "Spin-Pinion" or "Spool-Pinion). Next there is a ring of corresponding teeth that the Spinion can roll along, in order to produce spin every time we flip. Probably unsurprisingly, this new component is called the "Spin Ring".

The ratio of these gears has been set to nominally produce 180° of spin during the flip. Actually this is 180° of net spin, as it really spins 900° in total, but every 360° is a net of zero because it puts the die back into the position it started in. We only really care about the net spin here, because that's what determines which face we land on, so that is what I will refer to going forward. 

As we saw above, 180° of spin is what we need in order to go from 4 -5 and from 9-0. The other two net spins (positive and negative 108°) are achieved in the device by rotating the Spin Ring itself! If we rotate the Spin Ring in the same direction as the flip, then the Spinion will see fewer ring teeth along its flip journey and therefore spin less. Conversely, if we rotate the Spin Ring in the opposite direction it will see more ring teeth and spin further.

We can see now why it was useful before to start thinking about our original 108° and 252° spins as actually ±108°. Because now we only actually have one Spin Ring rotation distance that we need to generate. We need it in two different directions, but the distance is the same in both cases.

It may not always be easier to switch output directions in a mechanism vs changing the output "distance", but in this case there is a neat feature of bevel gears that we can exploit to make the direction switching actually quite trivial. That is the fact that an input gear driving at the top of the output gear will produce an opposite rotation compared to driving it at the bottom, without changing the original input direction.

To take advantage of this, the device has two input bevel gears with alternating toothed and un-toothed segments that hand off control of the Spin Ring back and forth. There is also a region where both of the input gears have no teeth, in which the Spin Ring will not rotate, producing the net 180° spin.

All that's really left is to ensure this new system has an appropriate ratio to achieve the correct amount of output rotation at the Spin Ring. We need a pretty high ratio, so I have opted for a planetary gear system to get us there without taking up too much room. The sun gear is directly driven by the input knob, while the planets are fixed, and the internal ring gear teeth are built in to the input bevel gears.

Another great thing worth mentioning about this system is that it is entirely reversible by simply rotating the input knob in the opposite direction. So we can easily count up or down without having to engage or toggle any additional mechanisms to reverse the output. This would not be the case with a different form of input, like a reciprocating plunger/button, or lever. 

Hold Steady

There's one more major problem we need to solve here, which careful readers may have noticed. I kind of glossed over the fact that there is a configuration where neither of the input gears are engaged with the output (i.e. Spin Ring). This means that there’s nothing to keep the Flip Carrier from simply dragging the Spin Ring along with it during the flip.

To prevent this I added a spring detent system, with some spring tabs in the housing that engage with corresponding notches on Spin Ring. There are notches to hold at each of the other Spin Ring positions as well for consistency. I added a similar spring detent to the Flip Carrier, which further helps everything snap into place and hold at the correct configuration for each increment. It also acts as a kind of linchpin to retain the Flip Carrier and Spin Ring from simply falling out of the assembly.

Ok But Why Tho?

Now that we have a grasp of how this thing works, I think we have established the right context in which to discuss some of the "whys".

For example, why did I spend any of my precious time on this earth making this maybe-cool, but definitely not essential device?

First and foremost, it was fun and it was hard! When I first started thinking about this concept it was clear pretty quickly that this would be a genuinely interesting design challenge, and that alone is enough to earn a spot on my "potential future projects" list.

Additionally, as far as I can tell, it seems to be a unique/original idea. I could not find any examples of something like this already having been made. Plenty of other mechanical counters, and lots of spindown dice, but nothing quite like this.

However, when I first considered the idea, it wasn't originally just a counter...

Counting... Time?

Initially, I was thinking about the fact that a standard d10 has 0-9 instead of 1-10, which would make it uniquely suited to act as a digit in a clock. A typical digital clock has 4 digits that cycle through 0-9, so 4d10s would fit perfectly there.

But wait! The hours only really need up to 12 so why not use a d12 there and ditch one of the 4 digits entirely. With a d12 and two d10s we could have a pretty kick ass clock.

Ok so, a clock! A cool dice-based, digital mechanical clock! But where to start? Well we would need to figure out how to hold and manipulate each die. And since there would be two d10s, and also because those ought to be easier to hold and increment, we can start by figuring out how a single d10 digit will need to work. So then a sub-scale prototype that can cycle a d10 from 0-9 and back to 0. Well that's really just a single-digit counter, which is a pretty neat thing all on its own! 

And that's how this counter design was initially conceived: as step one in building a clock. After all what is a clock but a specialized counter that counts time...

What Next?

Many folks have already expressed interest in printing and/or owning one of these themselves, and I definitely do want to make that happen. I still have a bit of work to do though, to make sure this worthy of your print time and material (let alone your hard earned dollars).

Mainly I would like to improve the print-to-print repeatability of the current version. Plus there is one component that is at some risk of breaking if actuated to "enthusiastically". I would anticipate these concerns to become even more pronounced as others attempt to print this with their own setups.

I also have hopes for a V2 with one or more major design upgrades that were originally "requirements" but later abandoned:

One Handed Operation

Initially, I really wanted to be able to operate it with one hand. A good counter should ideally not slow down the activity that it is aiding by requiring cumbersome handling on each increment.

I did spend some significant time and effort on the one-handed concept, and while it was painful to have to admit, ditching that requirement ended up being the best decision for the project. But it was not a total loss, and certainly not a waste of time. It was during this phase that I developed some of the core systems including the die-holding spools, the Spinion & Spin Ring system, and the Flip Carrier, which were all carried over into the knob version mostly unchanged. Eventually though, I simply had to acknowledge that the design was not progressing as it should, and the compromises and complexity being added in the name of a not-really-real requirement were getting hard to justify.

I won't go into full detail here about this discarded version, but I can pretty well sum it up with one word: ratchets... ratchets on ratchets inside of ratchets... The thing sounded cool as hell, but didn't do its job all that well.

Now that I do at least have a working device, I have some ideas how to implement the one-hand version without sacrificing the "dueling bevel" solution, which really seems hard to beat at this point. Adding more parts and mechanical interfaces is not ideal, but in this case I think the payoff could be worth it.

Modularity

Originally, I thought it would be super neat to make this device fully modular, such that any number of these identical single-digit counters could be linked up side-by-side to create a counter of any size. I still think that's super neat, but at the point that I decided to abandon the one-hand path, I also made the decision to put this one on hold as well. Modularity is not so handy if the individual digits don't even work to begin with.

In looking forward to V2 though, I still have a desire to either implement true modularity, or at least build a fixed two-digit version of this counter.

The Clock!?!

Yes, I hear you: "What about the clock!?!?!"

The version of the clock concept that basically just uses four of these d10 counters is pretty straightforward and there's a reasonable chance I'll go ahead and put that together at some point in the future. One thing I don't love about it is how far apart the digits would have to be to accommodate each of their Spin Rings. I worry this would make it somewhat awkward to read, and just look a little weird in terms of its overall proportions. The masochist in me is working hard internally to justify a more fundamental re-design in order to hold a more natural/familiar digit spacing.

And then there is the d12-hour version... The one that kicked this whole thing off, and that still just makes so much sense (to me and apparently to many others who commented about this on the Reddit post). The major problem with this one though is that despite the complexity required to make the current version work, the d10 actually has a number of things going for it that make it especially good for this purpose.

Designing a d12 version is not simply a matter of adapting the current approach to accommodate two additional faces. It requires a completely different concept, and one that is certainly much more complicated. 

That said I may still attempt it one day! In the meantime, any intrepid tinkerer that solves this one themselves will have major respect and props from me! 🫡

Epilogue

If you made it this far congrats and welcome to the "end" (stick around for the footnotes if you're not ready to leave yet)! This was such a fun and sometimes frustrating project, and I am thrilled with the interest and reception it has received so far. I hope you found this post interesting and informative, and I'd love to be able to share the device itself more widely in some capacity or another, so if you have any interest in that stay tuned (subscribe below for email updates if you'd like). There are so many other design features, decisions, and iterations than I could reasonably include here, so feel free to drop a comment if there's anything you want to know more about!

For now, enjoy one more GIF for the road!

Footnotes

1. ⇧

   Welcome to the footnotes section. Click the arrow above to return to where you left off in the main body of the post

2. ⇧

   The faces are labeled 0-9, but generally the 0 is taken to be a 10 when this die is rolled on its own (there are also 1-10 d10s). When rolled together with a 00-90 the pair are called "percentile dice" (d%*) and can yield a value from 1-100.
   
   *Sub-footnote: The 00-90 itself is sometimes called the percentile die, but this would not be quite right technically. "Decile die" would be closer, or "Tens dice" which is pretty common.

3. ⇧

   The d10 is actually kind of an interesting case among the set of standard dice used in D&D (and other games). With the exception of the d10 (and it's 00-90 sibling), all of the other standard dice geometries (d4, d6, d8, d12, d20) are what are called "Platonic solids" (after Plato). We'll skip the geometry lesson about what exactly that designation entails, but its worth reading up on if you're interested. For our current context, the most important thing about Platonic solids is that (simply put) every face and every edge and every angle are identical. This makes them highly symmetrical and there is no face/edge/angle or orientation that is "preferred" over any other. You might be starting to understand why Platonic solids are perfect for use as dice: No face or orientation is special, so the odds of landing in any face-down orientation when tossed are totally even (in theory). 

   Unfortunately there are exactly 5 Platonic solids, and none of them have 10 sides. For this reason, there was not originally a d10 used in D&D (officially). But in our base-10-centric world it was inevitable. In fact, now there are TWO 10-sided dice in the standard set (see the note above this one). Prior to this a d20 could be used to produce a 1-10 result, and there were even d20s made with duplicated 1-10 numbering specifically for this purpose.

4. ⇧

   In fact realistically this could never have been the case. One thing we know about the standard d10 designs is that any pair of opposing faces will add up to 9 (0+9, 1+8, 2+7, etc.). There are a number of different ways to then arrange these pairs, but this rule remains constant for most d10 designs (one exception being those numbered 1-10, which generally sum opposing faces to 11).

   Lets take as an example, the increment from 4 to 5. These values are on opposite sides of the die (because 4+5 = 9), so we do need 180° of spin (in addition to the flip) to get from one to the other. That works great for 9 to 0 as well if we want to restart at the end of the count, since 9 + 0 also equals 9. But that's where it ends. None of the other opposing face values are sequential like this, so spinning 180° in any of the other scenarios will not get us what we want.

5. ⇧

   If there is another one already in existence I would LOVE to see it!!! There is a true thrill in seeing the different ways other people have found to solve similar problems.

6. ⇧

   A "spindown" die, has its numbers arranged sequentially, such that the "next" value is always adjacent to the current one. These are designed specifically for use as counters! I could have designed this device to use a die like that and potentially greatly simplify the mechanism, but that would not be as fun, nor as challenging and if we are being honest those are the top two reasons for this thing to exist so, yeah, hard pass. Its also just slightly less interesting (and slightly less useful even) to turn a counter into a different type of counter. I wanted this to be something that a person could make use of even if all they had was a standard set of polyhedral dice.

7. ⇧

   We can also consider the fact that the tens digit for the minutes only needs 0-5, so we could potentially use a six sided die there. The only real problem with that is that a d6 usually goes from 1-6, not 0-5, so we'd need a special die there. Which is not crazy, but not really in keeping with the theme of "a clock that tells time using dice that a lot of people already have laying around", and the ability for a person to swap in their own favorite dice is a feature that's just too good to pass up in my opinion.

8. ⇧

   Actuating the right-most digit would increment its left-hand neighbor each time it rolled over from 9 to 0, and similarly on down the line. It could also still retain the ability to directly actuate any individual digit, in order to increment by 10, or 100, etc, when so desired.

9. ⇧

   Geometrically, the d10's two-pyramid shape creates an incredibly natural option for holding the die by its two points. Every face on the die is a part of one of these two points, so every face can be presented in exactly the same way when it is their turn in the count. Additionally, this naturally preferred orientation is carried over into the orientation of the numbers on each face. They are set to be right side up when their associated point is up. This along with the fact that the even and odd numbers are grouped on to the two distinct halves is the reason that we can get away with flipping the die a constant 180deg for each increment.

   The d12 has absolutely none of these features. It has no naturally preferred halves or orientation (most other dice are like this by design by the way), and if you choose two of its points to grip from, you will have 6 faces that are in contact with the grippers, but 6 others that are totally free. In addition to "flip" and "spin" actions, you'd need to add another (e.g. "tilt") in order to have a consistent display orientation. It may even need an additional set of grippers or similar system with the ability to hand off the die in order to regrip at a different point.